[ cross-posted from zenpundit.com — another runup to the glass bead game ]
Below you can read my submission to the wonderful 3 Quarks Daily “web aggregator” site as a candidate to join their regular Monday blogging team — it didn’t even make their “close but no cigar” list, but I wrote it and I like it, so I’m posting it here.

___________________________________________________________________________________________________
.
They are both fine American authors, stylists of high repute yet little known, Annie Dillard and Haniel Long, but I hadn’t associated the two of them particularly closely until that day. I’d snarfed up a copy of Long’s Letter to Saint Augustine from the dollar box at Pasadena’s magnificent Archives theological bookstore, and on my way home to nearby Eagle Rock, stumbled on a passage that seemed hazily familiar.
My friend Jens Jensen, who is an ornithologist, tells me that when he was a boy in Denmark he caught a big carp embedded in which, across the spinal vertebrae, were the talons of an osprey. Apparently years before, the fish hawk had dived for its prey, but had misjudged its size. The carp was too heavy for it to lift up out of the water, and so after a struggle the bird of prey was pulled under and drowned. The fish then lived as best it could with the great bird clamped to it, till time disintegrated the carcass, and freed it, all but the bony structure of the talon.
By the time I arrived back at my books, I knew it was Annie Dillard I’d been reminded of, and a quick, no, excited but fumbling search turned up this passage from her Teaching a Stone to Talk:
And once, says Ernest Seton Thompson–once, a man shot an eagle out of the sky. He examined the eagle and found the dry skull of a weasel fixed by the jaws to his throat. The supposition is that the eagle had pounced on the weasel and the weasel swiveled and bit as instinct taught him, tooth to neck, and nearly won. I would like to have seen that eagle from the air a few weeks or months before he was shot: was the whole weasel still attached to his feathered throat, a fur pendant? Or did the eagle eat what he could reach, gutting the living weasel with his talons before his breast, bending his beak, cleaning the beautiful airborne bones?
They’re emblematic, those two quotes, the way I see them: emblematic in the sense that each could be the basis for a heraldic shield, the eagle stooping to carry off the weasel, air creature triumphant over creature of earth in the one, the fish dragging the bird down in the other — creature of water gathering the air creature into its own fatal realm.
Emblematic too, I see them, of the possibility of a rhyme between thoughts — and I have quoted them as such in previous essays, alongside rhymes of sound and rhymes of meaning, womb and tomb being the classic examples of choice, but also rhymes of image, the fan rotors and helicopter rotors in the opening sequences of Coppola‘s Apocalypse Now, rhymes of melody in counterpoint, in fugue… and rhymes, yes, in history, as when Sir Frederick Stanley Maude told the people of Baghdad in 1917, “Our armies do not come into your cities and lands as conquerors or enemies, but as liberators…” and Donald Rumsfeld chimed in, telling his own troops in that same weary city, almost a century later, “Unlike many armies in the world, you came not to conquer, not to occupy, but to liberate and the Iraqi people know this.”
Oh yeah?
*****
The world is woven, Jung tells us in one of his most original and illuminating insights, of woof and warp, causaland acausal principles , it is at once at every point synchronic and diachronic.
Moving through time, we have the causal, diachronic principle, one things leads to another: let us sort and analyze the actions of one thing on another until psychology becomes sociology, sociology turns into evolutionary biology, biology into genetics, genetics a form of chemistry that is essentially physics — and physics, at the quark-level at last, a matter of statistics, mathematics unfettered even by the dualism of wave and particle.
Let me be clear about this. I do not begrudge Higgs his boson or his Nobel, nor Chandrasekhar his Nobel or his limit. But both men followed the warp, the causal, time-bound length-wise threads of discovery to their fraying edges. And the causal threading of events, time’s warp in our lived universe, is the mode best suited to quantity, to the determinable, and knows little of mystery unless magnitude alone — the infinities of astronomy, the infinitessimals of subatomics, alone will qualify.
Oh, scale is a marvel, true enough — but it is quality, not quantity, where the mystery and the greater meaning resides.
*****
And so we come to the mind’s other faculty, the other manner in which the world is woven, the manner of rhyme and repetition, synchronicities and semblances, of patterns recognized within and across disciplines. The cross-weave.
This has been the step-child of cognition for too long — but with the rise of cybernetics, feedback loops, complexity theory, network thinking and multi-causality, we can no longer think only in linear progressions, but must also cultivate associative, lateral, sideways thinking — in short, creative leaps.
Creative leaps occur when we recognize commonalities across conceptual distances — theme and variations, as musicians would say, rhymes in the nature of things, multiple perspectives and voices in counterpoint. So the nature of our current world, in all its complexity and variegation, calls for what I would call a music of ideas.
I’m not the first to have this idea, Glenn Gould was pursuing it in his work for radio, blending the many voices and conversations in a train compartment, or at the different tables in a truck-stop café, to form an interwoven whole that comprehended all of its voices, all of its parts in a greater music. But it is Edward Said — another musicians, when he was not occupied with Israeli-Palestinian politics or literature — who observed in an essay in Power, Politics and Culture, p. 447:
When you think about it, when you think about Jew and Palestinian not separately, but as part of a symphony, there is something magnificently imposing about it. A very rich, also very tragic, also in many ways desperate history of extremes — opposites in the Hegelian sense — that is yet to receive its due. So what you are faced with is a kind of sublime grandeur of a series of tragedies, of losses, of sacrifices, of pain that would take the brain of a Bach to figure out. It would require the imagination of someone like Edmund Burke to fathom.
So that’s the symphonic scope of the thing, seeing the whole with all its fractures and dissonances as a music — a music that calls for harmonization, but remains in complex counterpoint.
*****
Hermann Hesse was the first great proponent of the music of ideas, at least in modern western times, and his glass bead game — evoked but never defined in his Nobel-winning novel of that name — offers us a glimpse both of the nature of moves and of the possible grandeur of an implicit world-architecture, formed of resonances and semblances, rather than of causes and effects.
Hesse gives us an insight into how the game is played at the level of moves and themes when he says a given game might have explored “the rhythmic structure of Julius Caesar’s Latin and discovered the most striking congruences with the results of well-known studies of the intervals in Byzantine hymns” — but he could hardly have known, back in the 1940s, that in 1978 the University of Wisconsin Press would publish Jane-Marie Luecke OSB’s monograph, Measuring Old English Rhythm: an Application of the Principles of Gregorian Chant Rhythm to the Meter of Beowulf. Intentionally or unintentionally, his game is played by all whose minds play with meanings. And there’s a game move right there, in the conviviality between the fictional move of Hesse himself, and the monograph, years later, of a Benedictine nun.
Tiny, you say, a tiny move — but a move in what Hesse termed the “hundred-gated Cathedral of Mind.”
And the scope of that cathedral, in its gradual entirety, is vast — encompassing all the vast quantities of the sciences, with the qualitative depths and heights of the arts and humanities too:
The Glass Bead Game is thus a mode of playing with the total contents and values of our culture; it plays with them as, say, in the great age of the arts a painter might have played with the colors on his palette. All the insights, noble thoughts, and works of art that the human race has produced in its creative eras, all that subsequent periods of scholarly study have reduced to concepts and converted into intellectual values the Glass Bead Game player plays like the organist on an organ. And this organ has attained an almost unimaginable perfection; its manuals and pedals range over the entire intellectual cosmos; its stops are almost beyond number. Theoretically this instrument is capable of reproducing in the Game the entire intellectual content of the universe.
We are drawing close, in a humanly possible way and without making any predications of the being or non-being of such a supposed entity, to the very mind of god.
*****
And with immediate real world application, as when Maxwell sees the commonality between electricity and magnetism, Kekulé the serpent-biting-it’s-tail like form of the benzene ring — or Taniyama‘s 1955 “surmise” as Barry Mazur puts it, that “every elliptic equation is associated with a modular form” — an insight that was to bear rich fruit forty years later, in Andrew Wiles‘ proof of Fermat’s Last Theorem.
Hesse’s vision of the game was lucid, elegant, intellectual — but lacked real world application. Viewed as a method of scoring the music of ideas, it offers illuminations from the most abstract and theoretical of mathematics to the most complex of opposed political intrangencies — from Tamiyama to Edward Said, and from Christopher Alexander‘s Pattern Language to John Holland‘s “genetic algorithms“. Alexander and Holland each indicate their debt to Hesse’s fictional game in their own respective works.
How, then, to notate this game, these moves that leap side-wise, pattern-wise, semblance-wise across boundaries and boxes, limitations and disciplines — for it is these leaps, as Arthur Koestler notes in his The Act of Creation, that give us the surprised aha! of discovery, the unexpected ha! of laughter, the gut-wrenching wail aiiyeee! when tragedy strikes.
My own inclinations favor play — solo or with a friend — at a coffee house, with pencil and paper napkin, with a small graph for a board, ideas played at its nodes, connections and resonances represented by its edges. I’m thinking of network mapping on a human scale, between seven and a dozen nodes, each one rich in meaning, anecdote, quote, statistic, image, snatch of song…
But the essence is the single move, the single resemblance. And for this I have a form which I would like to offer you, downloadable, for your own experiments:
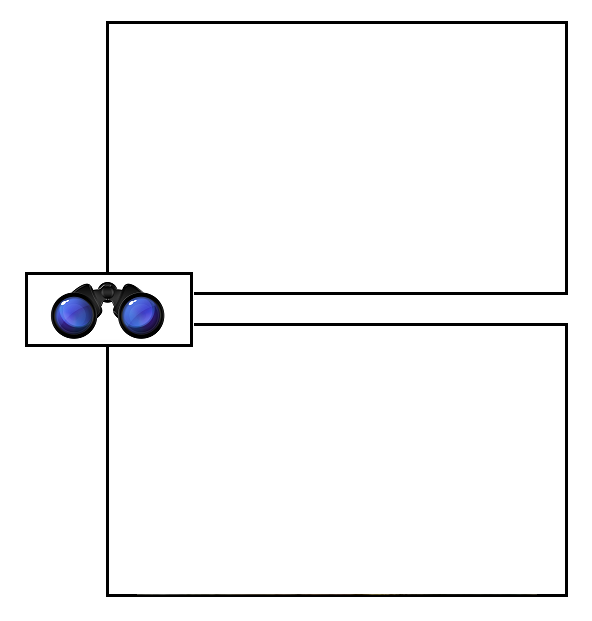
Download the image and fill the two spaces with what you will — whatever you can sketch, whistle, count out or scribble —
I think you’ll find the greatest reward comes when the two ideas, visuals, verbals, aurals you juxtapose are closely related yet drawn from distantly separated regions of thought.
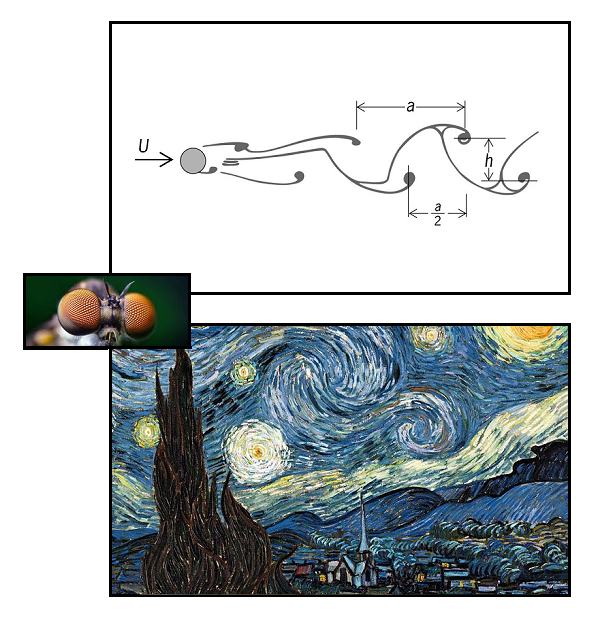
At their best, such juxtapositions cross galaxies. My own most cherished example to date compares a night sky by Van Gogh with a von Kármán diagram of turbulent flow…

*****
And where does this lead us? What becomes of CP Snow‘s famed Two Cultures?
Two great rows of pillars in Hesse’s hundred-gated cathedral, perhaps — best appreciated when one looks up, and sees the great vaulted roof, the magnificence of the arches between them.
In future Monday columns here on 3QD, I hope to bring you some further moves in the great game of correspondences, weaving together topics that have caught my attention in the preceding month — now in poetry, now on the morning news.
The leaps.
___________________________________________________________________________________________________

I’m happy to report that friend Bill Benzon made the 3 WQuarks Daily cut and will be blogging there, and that friend Omar Ali is already one of their regulars.


















 Andrew Wiles
Andrew Wiles